Viienda vooru kahe vigase ülesandega ülesannete komplekt osutus populaarseks. Esimese, teise, viienda ja kuuenda ülesande õigete vastusteni jõudsid ning neli punkti teenisid Sven-Erik Enno, Vladimir Jaanimägi, Aivar Kauge, Kalle Kulbok, Toomas Lausmaa, Katre Luik, Indrek Lüüs, Marko Orav, Meelis Reimets, Kuldar Traks, Hannes Valk, Mariina Viil ja Heldur Väljamäe. Vooruauhind läks seekord Martiina Viilile.
Vooru võitja saab kingituseks raamatu sarjast „Looduse raamatukogu“ või loodushäälte CD-plaadi. Sarjas ilmunud raamatutega ja CD-plaatidega saab tutvuda veebilehel www.loodusajakiri.ee ja eelistustest saab teada anda toimetuse telefonil 610 4105 või meiliaadressil loodusajakiri@loodusajakiri.ee.
| Nimi | I | II | III | IV | V | VI |
| Jaanimägi, Vladimir | 5 | 4 | 6 | 4 | 4 | |
| Kulbok, Kalle | 5 | 4 | 6 | 4 | 4 | |
| Reimets, Meelis | 5 | 4 | 6 | 4 | 4 | |
| Sammul, Siim | 5 | 4 | ||||
| Sõlg, Anti | 5 | 4 | 6 | |||
| Traks, Kuldar | 5 | 4 | 6 | 4 | 4 | |
| Tõnissoo, Toomas | 5 | 4 | 2 | 2 | ||
| Valk, Hannes | 5 | 4 | 4 | 4 | 4 | |
| Viil, Martiina | 5 | 4 | 6 | 4 | 4 | |
| Väljamäe, Heldur | 5 | 4 | 4 | 4 | 4 | |
| Kauge, Aivar | 4 | 4 | 6 | 4 | 4 | |
| Orav, Marko | 5 | 4 | 4 | |||
| Seljamaa, Jarmo | 4 | |||||
| Luik, Katre | 4 | 4 | ||||
| Lüüs, Indrek | 2 | 4 | ||||
| Lausmaa, Toomas | 4 | |||||
| Enno, Sven-Erik | 4 |
Viienda vooru vastustest
Eelmise vooru kolmanda ja neljanda ülesande puhul oli tegemist Macey Brooke’i väga heast ning äärmiselt usaldusväärsest krüptoarimeetika alasest ülesannete kogust “150 PUZZLES IN CRYPT-ARITHMETIC“ [Dover, 1963] pärit ülesandega nr 142.
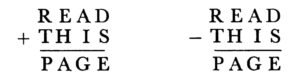
Brooke kirjutab selle ülesande juures: „Need on kaks erinevat ülesannet. See tähendab, et näiteks R-tähe väärtus liitmisel erineb R-tähe väärtusest lahutamisel jne.“
Seejuures esitab Brooke ainsate täiesti õigete tulemustena järgmised vastused:
3285 + 1607 = 4892 ja 5809 – 3741 = 2068.
Paraku tegi Tõnu Tõnso seda ülesannet üle võttes mitu rumalat viga. Esiteks ta lahutaski ühe ülesande kaheks erinevaks ülesandeks ning arvas naiivselt, et kui on tegemist kahe erineva ülesandega, siis järelikult võib neid esitadagi erinevate ülesannetena ja niiviisi kaob ka ühele tähele kahe erineva numbri vastamise probleem ära. Tegelikult kaotas ta niiviisi ära ka väga palju lahendusvariantide arvu piiravaid tingimusi. Kui näiteks esimeses ülesandes on R = 3, E=2 ja A=8, siis teises ülesandes R ≠ 3, E≠2 ja A≠8. Kui aga teises ülesandes on näiteks R = 5, E=8 ja A=0, siis esimeses ülesandes R ≠ 5, E ≠ 8 ja A ≠ 0 jne. Kuna variantide arvu piirav tingimus (iga tähe taga peituv arvväärtus peab kahe ülesande puhul erinev olema!) kadus, siis ilmnes, et esimese ülesandel puhul tekkis tervenisti 72, teise ülesande puhul aga lausa 96 sobivat ning tähtedele vastavat arvude komplekti.
Et Brooke’i raamat on krüptoaritmeetika klassika, siis teine Tõnu Tõnso andestamatu viga oli see, et ta ei kontrollinud kõike pärast ülesande kaheks lahkulöömist üle.
Vastused:
1) 138 x 138 = 19044
2) 625 = 54 ja 256 = 44
3) ja 4) ülesanne sai Tõnu Tõnso rumalate vigade läbi ära rikutud
5) 4 x 2178 = 8712
6) 6 x 1340 = 8040
